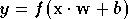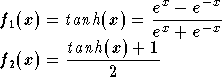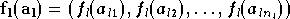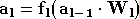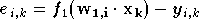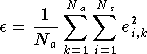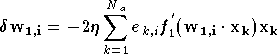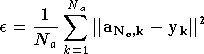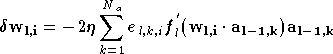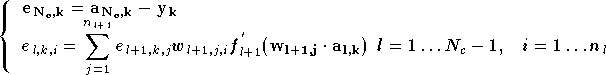Le perceptron multicouche (PMC) est la deuxième grande famille de réseaux de neurones. Après avoir décrit l'architecture de ces réseaux on va aborder leur apprentissage, et le concept de rétropropagation de l'erreur.
Un neurone de
perceptron réalise un produit scalaire entre son vecteur d'entrées
 et un vecteur de paramètres
et un vecteur de paramètres 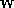 appelé poids, y ajoute un
biais
appelé poids, y ajoute un
biais
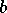 , et
utilise une
fonction d'activation
, et
utilise une
fonction d'activation 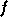 pour déterminer sa sortie [RUME86] :
pour déterminer sa sortie [RUME86] :
Les fonctions d'activation doivent être de préférence
strictement croissantes et bornées. Les fonctions classiquement
utilisées sont la fonction linéaire, la tangente hyperbolique (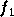 ) et la fonction
sigmoïde standard (
) et la fonction
sigmoïde standard (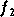 ) :
) :
La différence entre ces deux dernières fonctions est le domaine
des valeurs prises, qui est de 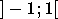 pour la tangente hyperbolique et de
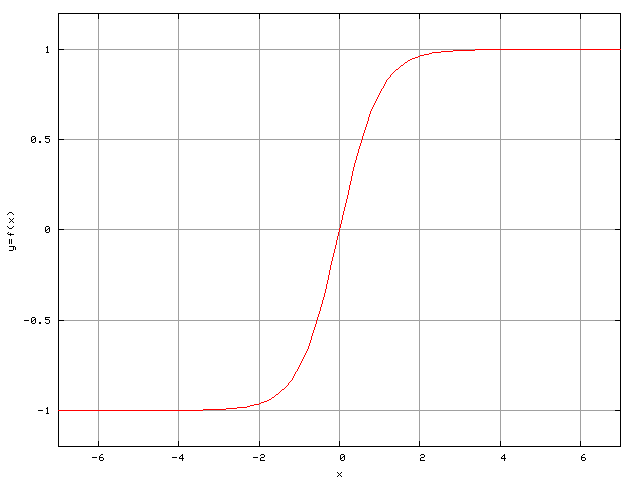
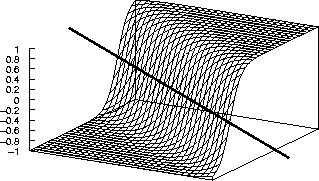
pour la tangente hyperbolique et de 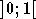 pour la sigmoïde standard. La figure 2.12 montre
la courbe de la tangente hyperbolique :
pour la sigmoïde standard. La figure 2.12 montre
la courbe de la tangente hyperbolique :
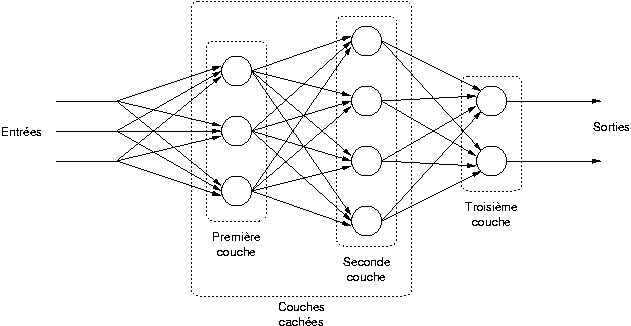
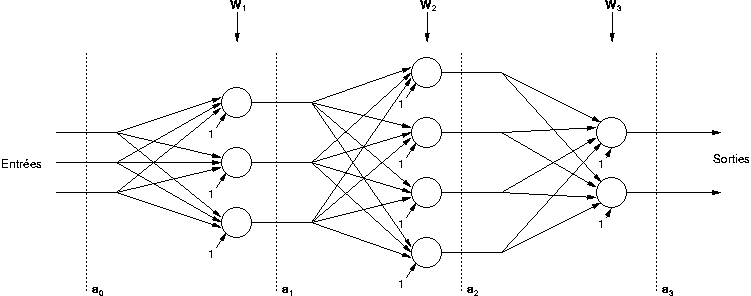
Le perceptron est organisé en plusieurs couches. La première couche est reliée aux entrées, puis ensuite chaque couche est reliée à la couche précédente. C'est la dernière couche qui produit les sorties du PMC. Les sorties des autres couches ne sont pas visibles à l'extérieur du réseau, et elles sont appelées pour cette raison couches cachées.
Notons 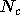 le nombre de couches. L'indice
le nombre de couches. L'indice 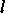 servira à désigner une couche, et notons
servira à désigner une couche, et notons
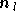 le
nombre de neurones dans la couche
le
nombre de neurones dans la couche 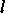 .
L'indice
.
L'indice 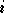 désigne un neurone. Le vecteur de poids du neurone
désigne un neurone. Le vecteur de poids du neurone
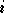 de
la couche
de
la couche 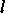 est noté
est noté 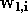 ,
et tous les vecteurs de poids d'une couche sont regroupés dans une
matrice
,
et tous les vecteurs de poids d'une couche sont regroupés dans une
matrice 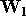 .
En ce qui concerne les biais, on les considère souvent comme un poids
supplémentaire associé à une entrée qui est toujours à 1. Ceci revient
exactement au même, mais permet de simplifier les notations, et
c'est donc ce que nous ferons dans le reste de ce mémoire. Notons
.
En ce qui concerne les biais, on les considère souvent comme un poids
supplémentaire associé à une entrée qui est toujours à 1. Ceci revient
exactement au même, mais permet de simplifier les notations, et
c'est donc ce que nous ferons dans le reste de ce mémoire. Notons
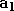 le vecteur regroupant les sorties des neurones de la couche
le vecteur regroupant les sorties des neurones de la couche
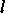 .
Comme chaque couche est reliée à la précédente,
.
Comme chaque couche est reliée à la précédente,
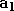 est également l'entrée de la couche
est également l'entrée de la couche
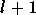 ,
en ajoutant l'entrée supplémentaire à 1 pour le biais. Par extension
notons
,
en ajoutant l'entrée supplémentaire à 1 pour le biais. Par extension
notons  l'entrée du réseau.
l'entrée du réseau.
Nous allons considérer de plus que tous
les neurones d'une couche ont la même fonction d'activation,
mais qu'elle peut différer d'une couche à l'autre. La
fonction d'activation des neurones de la couche
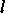 est
notée
est
notée 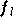 et on définit une extension vectorielle de
et on définit une extension vectorielle de
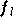 par :
par :
On peut alors écrire la relation suivante pour exprimer la sortie d'une couche en fonction de son entrée :
Le calcul de la sortie du perceptron multicouche se fait de
manière itérative. Il faut tout d'abord placer les entrées du réseau
dans le vecteur  ,
puis appliquer l'équation (2.18)
avec
,
puis appliquer l'équation (2.18)
avec 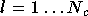 afin de calculer successivement
afin de calculer successivement 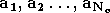 .
La sortie du réseau est alors
.
La sortie du réseau est alors 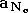 .
.
Les fonctions qu'il est possible de réaliser avec un PMC sont diverses. Dans un perceptron à une couche, il n'y a pas de couche cachée, et l'unique couche relie les entrées du réseau aux sorties. Si la fonction d'activation utilisée est une sigmoïde, chaque sortie est une sigmoïde de produit scalaire. L'espace d'entrée est donc coupé en deux par un hyperplan. La sortie est égale à 1 d'un côté de l'hyperplan et à -1 de l'autre côté, lorsque l'on est situé à une certaine distance de celui-ci. Pour des points situés près de l'hyperplan, la transition est progressive. Dans l'exemple simple d'un réseau à deux entrées et une sortie composé d'un unique neurone, l'hyperplan est une droite. La figure 2.15 montre la sortie de ce neurone (axe vertical) en fonction de ses deux entrées (axes horizontaux) :
Dans ce neurone, le biais fixe la distance entre l'origine et la droite (montrée figure 2.15), tandis que le vecteur poids (à deux dimensions) est orthogonal à la droite, et donc fixe sa direction, ainsi que la "largeur" de la zone de transition : plus le module du vecteur poids est élevé, plus la sortie évoluera rapidement de -1 à 1 en traversant la droite.
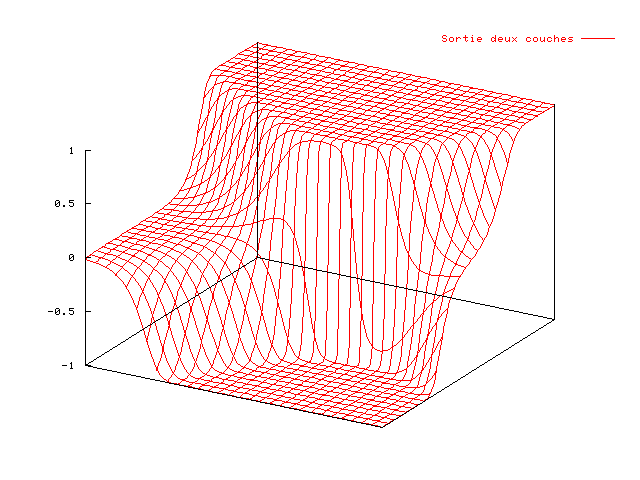
Dans un perceptron à deux couches, les sorties du réseau seront des combinaisons des sorties de la première couche, et on voit apparaître des intersections entre les zones définies par les neurones de la première couche.
De manière plus analytique on peut considérer la sortie d'une couche (équation (2.18)) comme une fonction vectorielle, dont les éléments constituent une base de fonctions. En ajoutant une seconde couche, les sorties sont des combinaisons des différents éléments de cette base, qui peuvent éventuellement servir à nouveau de base pour une autre couche. Il y a une ressemblance entre une couche de PMC, qui permet une décomposition dans une base de fonctions tangentes hyperboliques et une couche de GRBF, qui elle permet une décomposition dans une base de fonctions gaussiennes.
Il a été montré qu'un perceptron à deux couches avec des fonctions d'activation intégrables au sens de Riemann non polynomiales sur la première couche et une fonction d'activation linéaire sur la seconde est un approximateur universel [HORN93]. Comme pour le GRBF, ceci veut dire que le réseau est capable d'approximer n'importe quelle fonction douce avec une précision donnée, pourvu que l'on fournisse un nombre suffisant de neurones dans la couche cachée. Cependant en pratique il n'est pas forcément possible d'approximer toute fonction, car dans certains cas le nombre de neurones nécessaire peut être très important, et le théorème dans l'article cité ne garantit pas que l'algorithme d'apprentissage pourra converger vers le résultat souhaité.
L'apprentissage d'un perceptron se fait avec une descente de gradient, algorithme décrit en annexe, section 1. Dans le cas d'un perceptron à une couche l'expression de l'évolution des poids est assez simple. En effet l'erreur du réseau est de la forme :
où 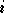 est le numéro de la sortie et
est le numéro de la sortie et 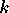 celui de l'exemple de la base d'apprentissage. La
performance du
réseau, une erreur quadratique moyenne, est :
celui de l'exemple de la base d'apprentissage. La
performance du
réseau, une erreur quadratique moyenne, est :
En appliquant à ces équations l'algorithme de descente du gradient ((A.1) et (A.2)), l'évolution des poids au cours d'une itération est donnée par [RUME86] :
Dans un perceptron multicouche il faut tenir compte de
l'influence de plusieurs couches dans le calcul du gradient.
Reprenons les notations utilisées dans la section 3.1, en notant
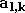 la sortie de la couche
la sortie de la couche 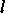 lorsque l'on applique en entrée l'exemple
lorsque l'on applique en entrée l'exemple
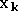 .
En notant de plus
.
En notant de plus 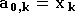 ,
on peut appliquer (2.18) pour
calculer tous les
,
on peut appliquer (2.18) pour
calculer tous les 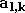 avec
avec 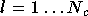 et
et 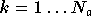 .
La performance du perceptron est :
.
La performance du perceptron est :
En appliquant l'algorithme de descente du gradient ((A.1) et (A.2)) à cette performance et en utilisant (2.18), on montre qu'une méthode itérative permet de calculer facilement le vecteur gradient. En effet, on peut exprimer l'évolution des poids sous la forme [RUME86] :
où le terme d'erreur
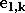 de composantes
de composantes 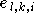 est de la forme :
est de la forme :
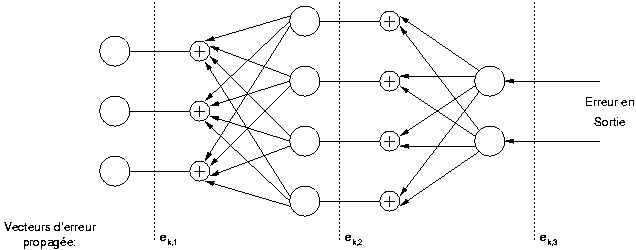
On constate que l'évolution des poids est similaire à celle vue pour le perceptron à une couche, en définissant une erreur sur chaque couche du perceptron. L'erreur de la dernière couche est effectivement l'erreur du réseau, et pour chaque couche cachée les erreurs sont calculées à partir des erreurs de la couche suivante. Pour chaque neurone l'erreur est la somme des erreurs de chaque neurone de la couche suivante, pondérée par le poids qui le lie au neurone dont on calcule l'erreur et par la dérivée de la fonction d'activation. Pour cette raison cet algorithme est appelé rétropropagation de l'erreur.
L'expression de la descente de gradient sous cette forme
permet une réalisation simple de l'algorithme. A chaque itération,
les différents vecteurs 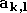 puis la sortie du perceptron
sont calculés en utilisant l'équation (2.18) en allant de la couche
puis la sortie du perceptron
sont calculés en utilisant l'équation (2.18) en allant de la couche
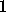 à la
couche
à la
couche 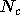 ,
puis les erreurs sont calculées en utilisant l'équation (2.24) en allant de la couche
,
puis les erreurs sont calculées en utilisant l'équation (2.24) en allant de la couche
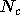 à
la couche
à
la couche 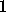 .
Enfin les poids de chaque neurone sont mis à jour en utilisant
l'équation (2.23).
.
Enfin les poids de chaque neurone sont mis à jour en utilisant
l'équation (2.23).
Lorsque l'on augmente le nombre de couches, on constate que l'algorithme d'apprentissage nécessite de plus en plus d'itérations pour converger vers un résultat. C'est pour cette raison que l'on dépasse rarement deux couches cachées dans un PMC. De plus une ou deux couches cachées suffisent généralement pour approximer ce que l'on veut. Si la descente de gradient est trop lente pour réaliser l'apprentissage, il est également possible d'utiliser un algorithme du second ordre, tel que celui de Levenberg Marquardt, présenté en annexe section 2. Dans ce cas chaque itération demande plus de calculs, mais dans la plupart des cas le nombre d'itérations nécessaires pour converger est bien moindre.
Un perceptron multicouche est capable d'approximer des fonctions de forme très différente. Contrairement au réseau GRBF l'approximation faite n'est pas locale, mais globale, et donc il sera plus adapté lorsque les vecteurs d'entrée ont une répartition assez uniforme dans l'espace d'entrée. Par contre si la fonction à approximer présente des variations assez localisées dans l'espace, un perceptron multicouche risque d'être plus complexe qu'un réseau GRBF avec les mêmes performances. Le choix du nombre de couches et du nombre de neurones est primordial dans un perceptron. En ajoutant des neurones ou des couches on améliore les capacités du réseau et donc la finesse de l'approximation, mais l'apprentissage devient plus long (particulièrement en augmentant le nombre de couches) et le risque de surapprentissage augmente. Généralement ces nombres sont déterminés expérimentalement, mais certains algorithmes itératifs existent également. On peut commencer avec un petit réseau et ajouter progressivement des neurones [BELI95], ou au contraire commencer avec un grand réseau et enlever des neurones [LUND97].