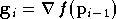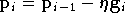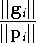L'algorithme d'optimisation le plus simple est la
descente de
gradient, dont le principe est de partir d'un point aléatoire puis de
se déplacer dans la direction de la plus forte pente. En appliquant un
certain nombre d'itérations, l'algorithme converge vers une
solution qui est un minimum local de 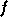 .
.
Figure A.1. Illustration du principe de la descente de gradient, dans le cas d'une fonction à une variable
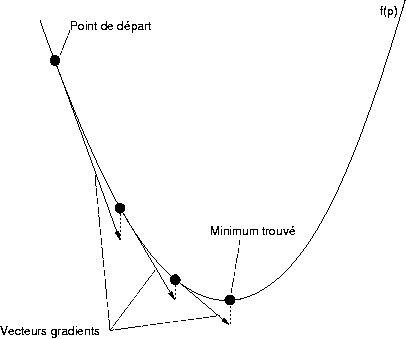
On commence donc par choisir un vecteur
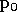 de manière aléatoire. Puis pour
l'itération numéro
de manière aléatoire. Puis pour
l'itération numéro 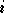 on calcule le gradient de
on calcule le gradient de 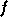 au point
au point 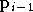 :
:
Le nouveau vecteur de paramètres calculé est :
où
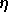 est
une constante qui ajuste la vitesse de
convergence de l'algorithme, déterminée empiriquement. Une fois le
nouveau vecteur
est
une constante qui ajuste la vitesse de
convergence de l'algorithme, déterminée empiriquement. Une fois le
nouveau vecteur 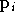 calculé on passe à l'itération suivante. Si
calculé on passe à l'itération suivante. Si
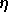 est
trop grande, l'algorithme n'est pas
stable et oscille autour d'une solution, et si
est
trop grande, l'algorithme n'est pas
stable et oscille autour d'une solution, et si
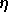 est
trop petite, un très grand nombre d'itérations sera nécessaire pour
converger vers la solution, et la probabilité de convergence vers une
solution locale est plus grande. Plusieurs
critères peuvent être définis pour arrêter l'algorithme : on
peut limiter à un certain nombre d'itérations, ou arrêter lorsque
est
trop petite, un très grand nombre d'itérations sera nécessaire pour
converger vers la solution, et la probabilité de convergence vers une
solution locale est plus grande. Plusieurs
critères peuvent être définis pour arrêter l'algorithme : on
peut limiter à un certain nombre d'itérations, ou arrêter lorsque
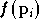 atteint un certain seuil minimal ou encore lorsque le vecteur évolue peu,
c'est à dire quand la valeur suivante atteint un seuil
minimal :
atteint un certain seuil minimal ou encore lorsque le vecteur évolue peu,
c'est à dire quand la valeur suivante atteint un seuil
minimal :
Ce dernier critère peut présenter le défaut d'arrêter l'algorithme trop tôt si la fonction présente des plateaux. Le choix du meilleur critère ainsi que le seuil à fixer est généralement trouvé de manière empirique. Il est également possible de prendre une combinaison de ces différents critères.
Le choix du coefficient 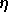 peut être délicat dans certains cas. Par exemple si
peut être délicat dans certains cas. Par exemple si
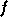 possède par endroits de grands plateaux, il faudrait avoir un coefficient
possède par endroits de grands plateaux, il faudrait avoir un coefficient
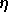 grand pour pouvoir s'en affranchir avec peu d'itérations. Si en
d'autres endroits
grand pour pouvoir s'en affranchir avec peu d'itérations. Si en
d'autres endroits 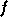 évolue au contraire très rapidement, il faut qu'il soit faible pour
que l'algorithme soit stable. Une variante peut être utile dans ce
cas, la
descente de gradient adaptative.
évolue au contraire très rapidement, il faut qu'il soit faible pour
que l'algorithme soit stable. Une variante peut être utile dans ce
cas, la
descente de gradient adaptative.
Dans une descente de gradient adaptative, le coefficient
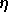 est
également ajusté à chaque itération, suivant l'évolution de la valeur
de
est
également ajusté à chaque itération, suivant l'évolution de la valeur
de 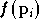 .
Si
.
Si 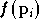 diminue, il est probable que l'on pourrait aller plus vite en
augmentant légèrement
diminue, il est probable que l'on pourrait aller plus vite en
augmentant légèrement 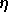 ,
et au contraire si
,
et au contraire si 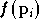 augmente, cela veut dire que le coefficient
augmente, cela veut dire que le coefficient
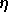 est
trop grand et qu'il faut le diminuer. Donc on décide d'augmenter
est
trop grand et qu'il faut le diminuer. Donc on décide d'augmenter
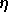 (de
10% par exemple) si
(de
10% par exemple) si 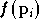 diminue, et de le réduire (en le divisant par 2 par exemple) si
diminue, et de le réduire (en le divisant par 2 par exemple) si
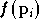 augmente. Cette approche permet généralement de réduire le nombre
d'itérations requis, et s'est révélée efficace avec tous les
réseaux de neurones que nous avons testés.
augmente. Cette approche permet généralement de réduire le nombre
d'itérations requis, et s'est révélée efficace avec tous les
réseaux de neurones que nous avons testés.
La descente de gradient peut être appliquée de deux manières lorsque
l'on évalue la fonction à l'aide d'une base d'exemples. La
méthode que nous avons employé, et décrite ci-dessus, est celle du
gradient total. Le vecteur 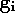 est calculé avec tous les exemples de la base d'apprentissage à chaque
itération, et le nouveau vecteur de paramètres est déterminé après avoir
parcouru toute la base. Dans une autre méthode, dite du gradient
stochastique, le vecteur
est calculé avec tous les exemples de la base d'apprentissage à chaque
itération, et le nouveau vecteur de paramètres est déterminé après avoir
parcouru toute la base. Dans une autre méthode, dite du gradient
stochastique, le vecteur 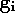 est calculé avec chaque exemple, et le vecteur de paramètres est recalculé
entre chaque exemple. Cette dernière méthode est particulièrement adaptée
aux systèmes dits online, pour lesquels les exemples sont communiqués
l'un après l'autre pendant l'optimisation, alors que pour la
méthode du gradient total il est nécessaire d'avoir la base complète
avant de commencer la première itération.
est calculé avec chaque exemple, et le vecteur de paramètres est recalculé
entre chaque exemple. Cette dernière méthode est particulièrement adaptée
aux systèmes dits online, pour lesquels les exemples sont communiqués
l'un après l'autre pendant l'optimisation, alors que pour la
méthode du gradient total il est nécessaire d'avoir la base complète
avant de commencer la première itération.