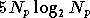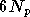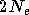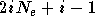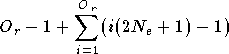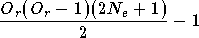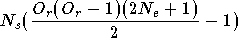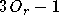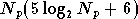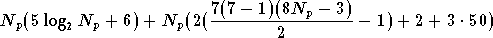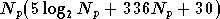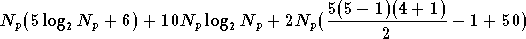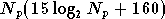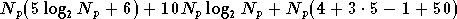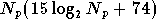Le correcteur dans le domaine fréquentiel n'a pu être efficacement entraîné que dans le cas d'un système à 4 porteuses. Avec 8 porteuses l'apprentissage commence à être difficile, et s'avère inefficace à 16 porteuses. Pour comparer les deux correcteurs nous avons donc pris un système à 4 porteuses, et analysé le taux d'erreur binaire dans les deux cas. Dans la figure 5.5, 'ref' indique le taux d'erreur binaire du système sans correcteur, 'rpn-f' celui obtenu avec un correcteur RPN dans le domaine fréquentiel, et 'rpn-t' celui dans le domaine temporel.
Figure 5.5. Taux d'erreur binaire en fonction du rapport signal sur bruit dans un système OFDM avec 4 porteuses, un amplificateur SSPA, un recul de 0 dB, une modulation MAQ16 et les correcteurs RPN fréquentiel et temporel
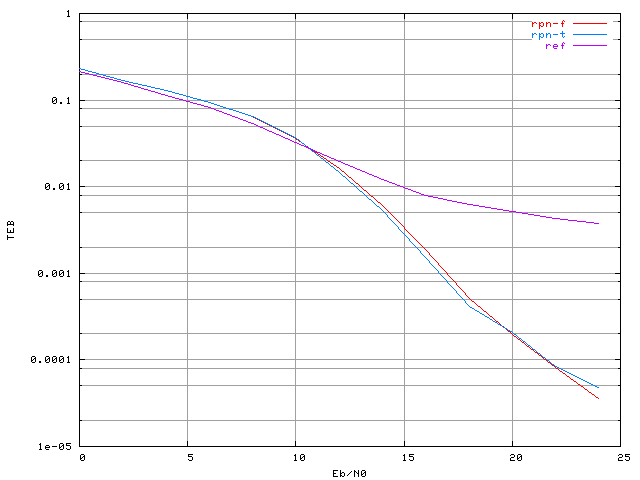
Les taux obtenus dans les deux cas sont quasiment identiques, les deux correcteurs ont les mêmes performances. Cependant il faut noter que sans amélioration de l'algorithme d'apprentissage, le correcteur temporel est actuellement le seul qui a de bonnes performances avec un nombre plus élevé de porteuses.
Le correcteur temporel utilise un réseau de neurones moins complexe que le correcteur fréquentiel, car il possède moins d'entrées. Mais il demande plus de calculs avant et après le réseau, puisqu'il utilise deux transformées de Fourier supplémentaires. On peut donc supposer que pour un petit nombre de porteuses le correcteur fréquentiel nécessitera moins de calcul, mais pour un nombre plus grand de porteuses c'est le correcteur temporel qui sera le plus simple. Afin de vérifier cette hypothèse, nous allons calculer le nombre d'opérations nécessaires dans chaque cas pour corriger un symbole OFDM.
Dans ce calcul, nous allons supposer que toutes les
opérations élémentaires (multiplication, division, addition,
soustraction) ont la même durée. Ceci n'est pas forcément le cas en
pratique, mais permet d'avoir une idée de la complexité des
différents algorithmes. Nous allons commencer par calculer le nombre
d'opérations élémentaires dans chaque étape de calcul. On rappelle
que 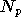 est le nombre de porteuses.
est le nombre de porteuses.
La
transformée de Fourier rapide est un algorithme qui permet de calculer
avec moins d'opérations une transformée de Fourier discrète dans
le cas où le nombre d'éléments est une puissance de 2
[BELL02].
Dans ce cas, la transformée est calculée en
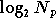 étapes, composées chacune de
étapes, composées chacune de 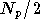 multiplications complexes et
multiplications complexes et 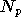 additions complexes, soit
additions complexes, soit 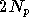 multiplications et
multiplications et 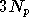 additions réelles. Le nombre d'opérations élémentaires est
donc :
additions réelles. Le nombre d'opérations élémentaires est
donc :
Si 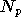 n'est pas une puissance de 2, nous l'arrondirons à la
puissance de 2 supérieure.
n'est pas une puissance de 2, nous l'arrondirons à la
puissance de 2 supérieure.
L'égalisation linéaire se fait dans le domaine fréquentiel,
avec 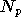 multiplications complexes, soit
multiplications complexes, soit 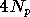 multiplications réelles et
multiplications réelles et 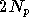 additions réelles. Le nombre d'opérations élémentaires est
donc :
additions réelles. Le nombre d'opérations élémentaires est
donc :
Soit un réseau RPN avec 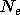 entrées réelles,
entrées réelles, 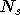 sorties réelles et d'ordre
sorties réelles et d'ordre 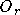 .
Ce réseau est composés de
.
Ce réseau est composés de 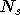 réseaux RPN qui calculent chacun une sortie. Chaque réseau RPN est
composé de
réseaux RPN qui calculent chacun une sortie. Chaque réseau RPN est
composé de 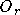 réseaux Pi-Sigma, d'ordres
réseaux Pi-Sigma, d'ordres 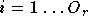 .
Enfin un réseau Pi-Sigma d'ordre
.
Enfin un réseau Pi-Sigma d'ordre 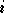 est constitué de
est constitué de 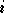 neurones Sigma, qui effectuent chacun un produit scalaire entre
l'entrée et un vecteur poids, et y ajoutent un biais. Donc un
neurone sigma nécessite
neurones Sigma, qui effectuent chacun un produit scalaire entre
l'entrée et un vecteur poids, et y ajoutent un biais. Donc un
neurone sigma nécessite 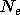 multiplications et
multiplications et 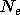 additions. Le nombre d'opérations d'un neurone Sigma est donc
:
additions. Le nombre d'opérations d'un neurone Sigma est donc
:
Un réseau Pi-Sigma d'ordre 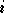 effectue le produit des sorties de ses neurones Sigma, soit
effectue le produit des sorties de ses neurones Sigma, soit
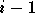 multiplications supplémentaires. Le nombre d'opérations d'un
réseau Pi-Sigma est donc :
multiplications supplémentaires. Le nombre d'opérations d'un
réseau Pi-Sigma est donc :
Un réseau RPN effectue la somme des sorties de ses réseaux Pi-Sigma. Son nombre d'opérations élémentaires est donc :
soit :
Et donc, pour les 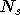 sorties du réseau RPN complet :
sorties du réseau RPN complet :
Ce calcul ne prend pas en compte la fonction d'activation.
Le calcul de la sortie d'un HPU d'ordre
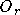 ,
si on ne prend pas en compte non plus la fonction d'activation,
revient à déterminer la valeur d'un polynôme de degré
,
si on ne prend pas en compte non plus la fonction d'activation,
revient à déterminer la valeur d'un polynôme de degré
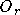 en un point. Les
en un point. Les 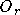 puissances consécutives de
puissances consécutives de  peuvent être réalisées avec
peuvent être réalisées avec 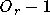 multiplications, puis ensuite il faut effectuer
multiplications, puis ensuite il faut effectuer
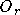 multiplications et
multiplications et 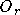 additions. Le nombre d'opérations d'un HPU est donc :
additions. Le nombre d'opérations d'un HPU est donc :
La tangente hyperbolique peut être calculée à l'aide d'une table de scrutation et d'un polynôme [TANG91]. Nous n'avons pas fait d'étude précise des opérations nécessaires à ce calcul, mais le nombre d'opérations est de l'ordre de quelques dizaines. Nous allons compter 50 opérations pour une tangente hyperbolique, en notant que la complexité de son calcul est généralement négligeable devant les autres opérations à effectuer, et une évaluation précise n'est pas nécessaire.
Ces calculs de complexité des différents éléments permet maintenant de déterminer celle des correcteurs eux-mêmes.
Un récepteur OFDM classique a besoin d'une transformée de Fourier et d'un égaliseur linéaire. Le nombre d'opérations demandées est donc (équations (5.2) et (5.3)) :
En plus du récepteur OFDM, le correcteur RPN fréquentiel
nécessite un réseau RPN d'ordre 7 à
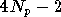 entrées et 2 sorties, avec une fonction d'activation qui est la
somme de 3 tangentes hyperboliques (dans le cas d'une MAQ16). Ce
réseau est utilisé
entrées et 2 sorties, avec une fonction d'activation qui est la
somme de 3 tangentes hyperboliques (dans le cas d'une MAQ16). Ce
réseau est utilisé 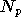 fois pour corriger les porteuses. Le nombre d'opérations requis
est donc (équations (5.10) et (5.8)) :
fois pour corriger les porteuses. Le nombre d'opérations requis
est donc (équations (5.10) et (5.8)) :
soit :
Le correcteur RPN temporel ajoute au récepteur OFDM deux
transformées de Fourier, un RPN d'ordre 5 à 2 entrées, 2 sorties,
et une fonction d'activation en tangente hyperbolique. Le RPN et
la fonction d'activation sont dans le domaine temporel et doivent
être appliqués aux 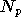 échantillons temporels du symbole OFDM. Le nombre d'opérations
requis est donc (équations (5.10), (5.2) et (5.8)) :
échantillons temporels du symbole OFDM. Le nombre d'opérations
requis est donc (équations (5.10), (5.2) et (5.8)) :
soit :
Pour le correcteur à HPU, en plus du récepteur OFDM et des deux transformées de Fourier, il faut déterminer le module du signal (2 multiplications, une addition, une racine carrée, donc 4 opérations), utiliser un HPU d'ordre 5 avec tangente hyperbolique, puis changer le module du signal (pour la partie réelle puis la partie imaginaire, une division par le module puis une multiplication par la sortie du HPU, donc 4 opérations au total). Le nombre d'opérations est donc de (équations (5.10), (5.2) et (5.9)) :
Soit :
Afin de déterminer de quelle manière ces complexités évoluent avec le nombre de porteuses du système OFDM, elles vont maintenant être représentées de manière graphique.
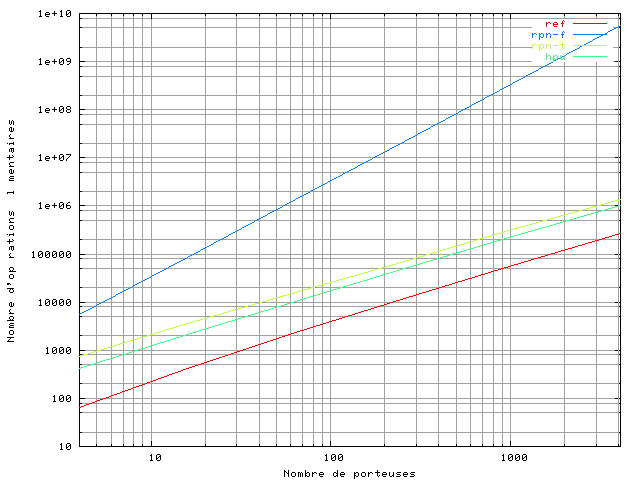
Nous pouvons maintenant tracer les courbes du nombre d'opérations nécessaires avec chacun des correcteurs en fonction du nombre de porteuses, dans la figure 5.6 :
La courbe 'ref' représente la complexité du récepteur OFDM simple sans correcteur. Contrairement à l'hypothèse de départ, même pour un faible nombre de porteuses, le correcteur RPN dans le domaine fréquentiel demande bien plus d'opérations que celui dans le domaine temporel. Les correcteurs RPN temporel et HPU demandent une puissance de calcul du même ordre de grandeur que celle requise par le récepteur OFDM, tandis que le correcteur fréquentiel en nécessite beaucoup plus. Enfin on remarque que la quantité de calcul du correcteur RPN temporel n'est pas beaucoup plus grande que celle du HPU. Les correcteurs temporels augmentent donc peu la complexité d'un récepteur OFDM.
Le correcteur dans le domaine temporel possède beaucoup d'avantages. Il demande moins de calcul à l'utilisation, a les mêmes performances que le correcteur fréquentiel tout en étant plus simple à entraîner. Le correcteur HPU a les mêmes performances que le correcteur RPN temporel, tout en étant encore plus simple pour son apprentissage et légèrement plus rapide à l'utilisation. Par contre le réseau RPN est plus général au niveau des types de non-linéarités gérées, alors que le réseau HPU peut nécessiter une adaptation.
Le seul défaut du correcteur dans le domaine temporel est qu'il ne peut compenser efficacement les non-linéarités apporté par un limiteur. Dans ce cas, le correcteur RPN fréquentiel peut être plus utile, à condition que l'on réussisse à résoudre les problèmes de l'apprentissage. En effet, un domaine typique dans lequel ce correcteur serait adapté est l'ADSL, qui utilise 256 porteuses, et dont le défaut non linéaire est une saturation du convertisseur numérique/analogique.
Le correcteur temporel est également plus rapide à entraîner. Le tableau suivant résume les temps d'apprentissage de différents réseaux présentés au cours de ce mémoire.
Tableau 5.1. Temps d'apprentissage des différents réseaux présentés
| Type correcteur | Type réseau | Algorithme | Temps |
| fréquentiel | PMC-30-25 | Descente gradient | 1 h 30 |
| fréquentiel | PMC-30-25 | Levenberg Marquardt | 70 h |
| fréquentiel | RPN ordre 7 | Descente gradient | 1 h 50 |
| fréquentiel | RPN ordre 7 | Levenberg Marquardt | 14 min |
| temporel | PMC-10 | Levenberg Marquardt | 2 min |
| temporel | RPN ordre 5 | Levenberg Marquardt | 30 s |
| temporel | HPU ordre 5 | Levenberg Marquardt | 8 s |