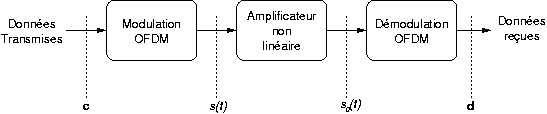
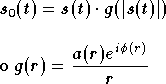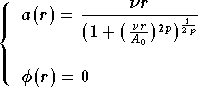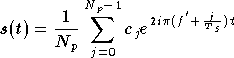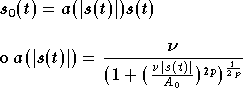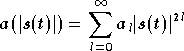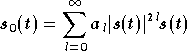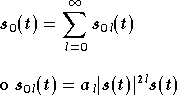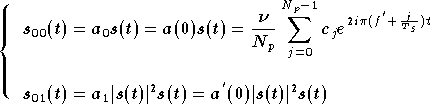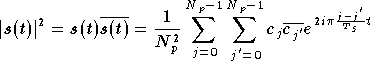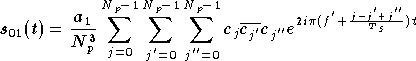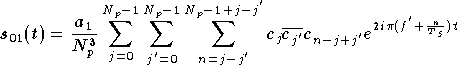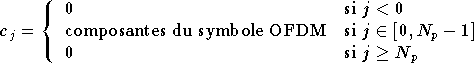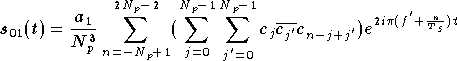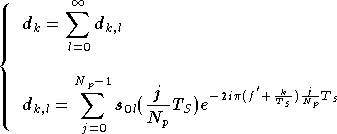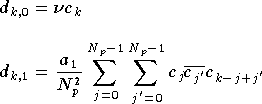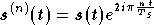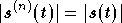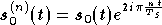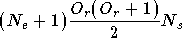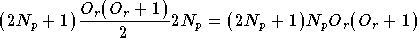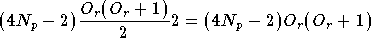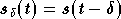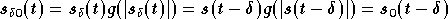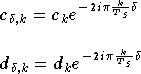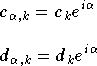En étudiant un système de communication numérique, on se rend compte qu'un système de compensation des non-linéarités peut être placé en divers endroits. Il est possible par exemple d'intervenir au niveau du codage source. Les réseaux de neurones ont déjà été étudiés pour le décodage source et il a été prouvé qu'ils peuvent accomplir cette tâche [CHAN98][JIAN95]. L'utilisation de réseaux de neurones pour créer ou utiliser un codage capable de corriger les erreurs particulières dues aux non-linéarités est un sujet de recherche intéressant mais ce n'est pas la voie qui a été choisie ici.
Il est également possible d'intervenir au niveau du canal. Dans les modulations monoporteuses, des réseaux de neurones ont été étudiés pour réaliser l'égalisation non linéaire de canal ainsi que la prédistorsion [LANG00]. La prédistorsion a déjà été évoquée dans le paragraphe 4.4, et son utilisation en multiporteuses est limitée par la saturation de l'amplificateur, puisque la puissance de crête du signal à amplifier est souvent bien supérieure à la puissance de saturation. Par contre l'emploi d'un réseau de neurones pour réaliser une égalisation non linéaire du canal semble plus intéressante pour une application en multiporteuses.
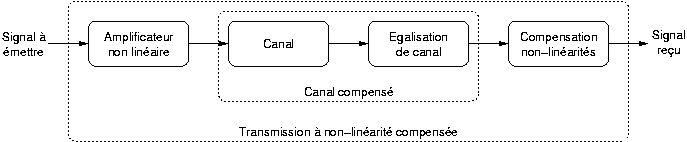
Comme évoqué dans la section 2.3, l'égalisation du canal en OFDM peut se réaliser très simplement, à l'aide d'une multiplication des symboles reçus. L'idée est donc de conserver cette simplicité, en séparant l'égalisation du canal et celle de la non-linéarité de l'amplificateur. La présence de blocs non linéaires dans la chaîne impose un ordre précis de ceux-ci. En effet les compensations doivent être placées dans l'ordre inverse de celui des effets compensés :
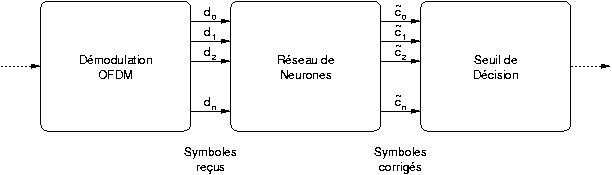
Ainsi le réseau de neurones sera inséré dans le récepteur OFDM après l'égalisation du canal et avant le seuil de décision et le décodage. La figure 3.2 présente le système plus en détail (TFD signifie Transformée de Fourier Discrète) :
Figure 3.2. Schéma d'un récepteur OFDM avec réseau de neurones pour la compensation des non-linéarités
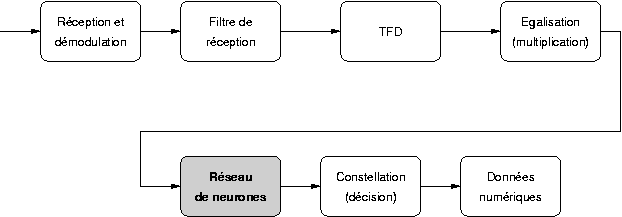
Le réseau de neurones travaille dans le domaine fréquentiel, et ne devra donc pas simplement réaliser une inversion de la fonction non linéaire temporelle de l'amplificateur : il devra prendre en compte les aspects fréquentiels de la non-linéarité.
Le but de cette section n'est pas de calculer précisément la non-linéarité dans le domaine fréquentiel, mais plutôt d'avoir une idée de son expression afin de déterminer comment le réseau de neurones devra être adapté.
Pour modéliser un amplificateur non
linéaire, on peut utiliser les
conversions AM/PM et AM/AM (AM : amplitude modulation,
PM : phase modulation). Si l'on appelle
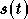 le signal à l'entrée de l'amplificateur et
le signal à l'entrée de l'amplificateur et
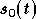 celui à sa sortie, ces conversions sont définies par :
celui à sa sortie, ces conversions sont définies par :
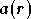 est la conversion AM/AM, ou non-linéarité d'amplitude, et représente
l'évolution du module de la sortie en fonction de celui de
l'entrée, le cas linéaire correspondant à
est la conversion AM/AM, ou non-linéarité d'amplitude, et représente
l'évolution du module de la sortie en fonction de celui de
l'entrée, le cas linéaire correspondant à
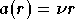 (où
(où 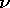 est le gain de l'amplificateur).
est le gain de l'amplificateur). 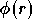 est la conversion AM/PM, ou non-linéarité de phase, et représente le
déphasage en sortie en fonction du module de l'entrée, le cas
linéaire correspondant à
est la conversion AM/PM, ou non-linéarité de phase, et représente le
déphasage en sortie en fonction du module de l'entrée, le cas
linéaire correspondant à 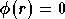 .
Un modèle utilisé pour les amplificateurs à semi-conducteurs est le SSPA
(Solid State Power Amplifier) [RAPP91] :
.
Un modèle utilisé pour les amplificateurs à semi-conducteurs est le SSPA
(Solid State Power Amplifier) [RAPP91] :
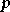 définit l'ordre de la non-linéarité, en général on choisit 1, 2 ou
3.
définit l'ordre de la non-linéarité, en général on choisit 1, 2 ou
3. 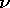 est le gain dans le domaine linéaire, et
est le gain dans le domaine linéaire, et
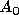 est l'amplitude de saturation (en sortie). La non-linéarité de phase
est nulle avec ce
modèle. D'autres modèles représentant des
amplificateurs présents dans les satellites (TWT pour Traveling-Wave
Tube, ou TOP pour Tube à Ondes Progressives) ont une non-linéarité de
phase non nulle.
est l'amplitude de saturation (en sortie). La non-linéarité de phase
est nulle avec ce
modèle. D'autres modèles représentant des
amplificateurs présents dans les satellites (TWT pour Traveling-Wave
Tube, ou TOP pour Tube à Ondes Progressives) ont une non-linéarité de
phase non nulle.
Pour l'étude de la non-linéarité de
l'amplificateur dans le
domaine fréquentiel, nous supposerons que l'égalisation du canal est
réalisée parfaitement, et donc allons retirer le canal de la
modélisation. Ensuite nous cherchons à exprimer le
symbole OFDM reçu 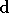 après égalisation du canal en fonction du symbole OFDM émis
après égalisation du canal en fonction du symbole OFDM émis
 .
.
Figure 3.3. Modèle utilisé pour le calcul de l'expression de la non-linéarité dans le domaine fréquentiel
Les composantes du symbole OFDM émis sont
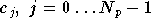 ,
et celles du symbole reçu
,
et celles du symbole reçu  ,
,
 étant le nombre de porteuses. Le signal temporel
étant le nombre de porteuses. Le signal temporel
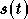 est la transformée de Fourier inverse du symbole OFDM (équations (1.19) et (1.20)) :
est la transformée de Fourier inverse du symbole OFDM (équations (1.19) et (1.20)) :
où 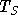 est la durée du symbole OFDM. Afin de simplifier l'écriture on ne
calcule la valeur du signal que pour le premier symbole OFDM, et donc on
ne s'intéresse qu'aux valeurs de
est la durée du symbole OFDM. Afin de simplifier l'écriture on ne
calcule la valeur du signal que pour le premier symbole OFDM, et donc on
ne s'intéresse qu'aux valeurs de
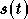 pour
pour 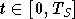 .
De plus la fréquence de la première
porteuse a été notée
.
De plus la fréquence de la première
porteuse a été notée 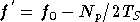 .
Le modèle d'amplificateur non linéaire que l'on va utiliser est
le modèle SSPA (équations (3.1) et (3.2)) :
.
Le modèle d'amplificateur non linéaire que l'on va utiliser est
le modèle SSPA (équations (3.1) et (3.2)) :
La fonction
 étant paire par construction[7], son développement en
série entière est
de la forme :
étant paire par construction[7], son développement en
série entière est
de la forme :
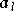 étant les coefficients du développement en série entière :
étant les coefficients du développement en série entière :
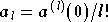 .
Et finalement l'expression du signal en sortie de
l'amplificateur non linéaire est :
.
Et finalement l'expression du signal en sortie de
l'amplificateur non linéaire est :
On ne peut pas calculer tous les termes de cette somme, mais il est possible de calculer les premiers. Posons
Les deux premiers termes ont pour expression :
La valeur de 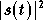 est :
est :
Et donc :
Et en appliquant le changement de variable
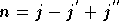 ,
on obtient :
,
on obtient :
On remarque tout d'abord que  varie de
varie de 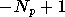 à
à 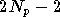 ,
suivant les valeurs de
,
suivant les valeurs de 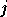 et
et 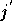 .
Si
.
Si 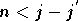 l'indice
l'indice 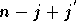 devient inférieur à
devient inférieur à  ,
et si
,
et si 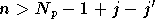 il devient supérieur ou égal à
il devient supérieur ou égal à 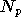 .
Donc si l'on étend la définition de
.
Donc si l'on étend la définition de
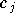 avec des coefficients nuls :
avec des coefficients nuls :
On peut alors écrire :
Ce qui nous permet de regrouper les termes par fréquence porteuse.
Les symboles reçus 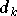 sont calculés avec la
transformée de Fourier de
sont calculés avec la
transformée de Fourier de 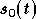 ,
et correspondent chacun à la
porteuse à la fréquence
,
et correspondent chacun à la
porteuse à la fréquence 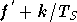 .
Comme pour
.
Comme pour 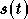 ,
on peut décomposer chaque
,
on peut décomposer chaque 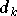 en une somme :
en une somme :
Chaque terme 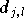 correspond à la contribution du terme
correspond à la contribution du terme 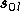 de la décomposition de
de la décomposition de 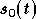 .
Les valeurs de
.
Les valeurs de 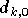 et
et 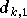 se déduisent facilement des équations (3.8) et (3.13),
puisqu'ils sont égaux à chaque fois au facteur de
se déduisent facilement des équations (3.8) et (3.13),
puisqu'ils sont égaux à chaque fois au facteur de
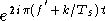 dans
dans 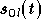 ,
multiplié par
,
multiplié par 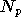 :
:
Les termes 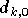 sont proportionnels aux symboles émis sur les différentes porteuses, et
correspondent à la composante linéaire du système OFDM. Les termes
sont proportionnels aux symboles émis sur les différentes porteuses, et
correspondent à la composante linéaire du système OFDM. Les termes
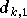 quand à eux sont proportionnels à une somme de produits 3 à 3 des
symboles émis, et correspondent à
l'intermodulation d'ordre 3. On peut montrer de même que les
symboles
quand à eux sont proportionnels à une somme de produits 3 à 3 des
symboles émis, et correspondent à
l'intermodulation d'ordre 3. On peut montrer de même que les
symboles 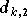 sont proportionnels à une somme de produits 5 à 5 des symboles émis, et
ainsi de suite.
sont proportionnels à une somme de produits 5 à 5 des symboles émis, et
ainsi de suite.
Dans un système OFDM classique les termes
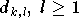 sont des perturbations qui vont augmenter le taux d'erreur binaire
de la transmission. Dans un système avec une compensation des
non-linéarités dans le récepteur, un module doit pouvoir inverser la
fonction
sont des perturbations qui vont augmenter le taux d'erreur binaire
de la transmission. Dans un système avec une compensation des
non-linéarités dans le récepteur, un module doit pouvoir inverser la
fonction 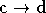 ,
c'est à dire retrouver les symboles émis
,
c'est à dire retrouver les symboles émis
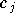 à
partir des symboles reçus
à
partir des symboles reçus 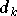 .
Le calcul précédent montre que le symbole reçu sur une porteuse ne
dépend pas uniquement du symbole émis sur cette même porteuse, mais
également de produits entre les symboles émis sur les autres porteuses.
Donc un réseau de neurones qui corrige la non-linéarité de
l'amplificateur sur une porteuse doit prendre en compte ce qui est
reçu sur toutes les porteuses, et en particulier les corrélations
d'ordre supérieur entre ces porteuses.
.
Le calcul précédent montre que le symbole reçu sur une porteuse ne
dépend pas uniquement du symbole émis sur cette même porteuse, mais
également de produits entre les symboles émis sur les autres porteuses.
Donc un réseau de neurones qui corrige la non-linéarité de
l'amplificateur sur une porteuse doit prendre en compte ce qui est
reçu sur toutes les porteuses, et en particulier les corrélations
d'ordre supérieur entre ces porteuses.
On a donc vu que le réseau de neurones a besoin des symboles reçus
sur toutes les porteuses pour compenser la non-linéarité. Il faudrait
donc choisir un réseau avec 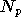 entrées et
entrées et 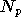 sorties, où
sorties, où 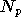 est le nombre de porteuses, dans le cas où le réseau de neurones est
capable de traiter des informations complexes. Si le réseau ne traite
que des informations réelles, il faut
est le nombre de porteuses, dans le cas où le réseau de neurones est
capable de traiter des informations complexes. Si le réseau ne traite
que des informations réelles, il faut 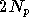 entrées et sorties réelles.
entrées et sorties réelles.
Cependant il est possible de chercher des symétries et des invariances dans le problème à résoudre, afin de simplifier cette structure. Tout d'abord on peut constater qu'il y a une invariance par décalage des porteuses. En effet si l'on crée le signal suivant :
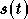 étant défini dans (3.3). On
constate alors que :
étant défini dans (3.3). On
constate alors que :
et donc :
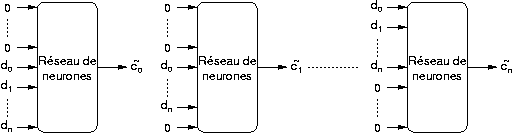
Ainsi lorsque l'on décale en fréquence les porteuses dans un système OFDM non linéaire, les porteuses reçues sont également décalées en fréquence, avec le même écart. Il est donc possible de créer un réseau de neurones qui ne possède qu'une sortie, et donc qui ne calcule le symbole corrigé que sur une porteuse. Les symboles corrigés sur les autres porteuses pourront être obtenus en décalant les entrées du réseau. Il faut donc ajouter des entrées au réseau de neurones afin de pouvoir réaliser ce décalage, décaler les entrées du rang voulu en fonction du symbole que l'on veut déterminer, et compléter les autres entrées à 0 :
Dans toutes les architectures testées, cette méthode permet de réduire de manière significative le nombre de poids, et donc d'augmenter la vitesse de convergence de l'apprentissage du réseau, et de réduire la puissance de calcul utilisée ainsi que le nombre d'exemples nécessaires dans la base. Dans le cas du réseau RPN (section 4.5) le nombre de poids nécessaires du réseau est :
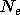 étant le nombre d'entrées,
étant le nombre d'entrées, 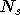 celui du nombre de sorties, et
celui du nombre de sorties, et 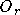 l'ordre du réseau. En effet un réseau RPN est composé de
l'ordre du réseau. En effet un réseau RPN est composé de
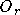 réseaux pi-sigma, d'ordres
réseaux pi-sigma, d'ordres 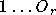 et dont le nombre de poids est donné dans l'équation (2.28). De plus pour réaliser
et dont le nombre de poids est donné dans l'équation (2.28). De plus pour réaliser
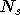 sorties il faut
sorties il faut 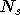 réseaux RPN. Donc dans le premier cas le nombre de poids nécessaires
pour le réseau est de :
réseaux RPN. Donc dans le premier cas le nombre de poids nécessaires
pour le réseau est de :
Et dans le second cas, avec décalage (on doit ajouter
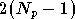 entrées et il n'y a plus qu'une sortie complexe, donc deux
sorties réelles) :
entrées et il n'y a plus qu'une sortie complexe, donc deux
sorties réelles) :
Le nombre de poids a donc été divisé par presque
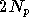 lorsque
lorsque 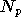 est assez grand.
est assez grand.
Maintenant si l'on suppose que deux symboles OFDM temporels
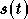 et
et 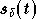 diffèrent uniquement par un retard
diffèrent uniquement par un retard 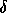 ,
c'est à dire que :
,
c'est à dire que :
alors on a à la réception :
Le système OFDM non linéaire est donc à temps invariant, c'est à dire que
lorsqu'un retard est
présent en entrée du système OFDM non linéaire, le signal en sortie aura
le même retard. Si l'on traduit cette propriété en fréquentiel, en
notant respectivement  et
et 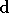 les symboles OFDM émis et reçu dans un cas, et
les symboles OFDM émis et reçu dans un cas, et
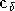 et
et 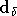 les symboles émis et reçus avec un retard
les symboles émis et reçus avec un retard
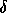 :
:
Avec le même raisonnement, on constate que si l'on applique
une rotation aux
symboles, c'est à dire que si on les multiplie tous par un complexe
de module 1, par conservation du module de
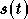 on observera la même rotation dans les symboles reçus. C'est-à-dire,
avec une notation similaire à la précédente :
on observera la même rotation dans les symboles reçus. C'est-à-dire,
avec une notation similaire à la précédente :
Les deux propriétés (3.24) et (3.25) sont vérifiées par le système OFDM non linéaire, et doivent être prises en considération pour faciliter l'apprentissage du réseau de neurones. Deux méthodes sont envisageables. Tout d'abord il est possible de modifier la structure du réseau de neurones afin qu'il vérifie ces propriétés de manière intrinsèque. L'article [GILE94] expose quelques idées pour construire des réseaux d'ordre supérieur présentant certaines invariances géométriques, mais les méthodes dépendent de l'architecture du réseau, et peuvent être complexes à mettre en oeuvre. Une autre méthode consiste à augmenter la taille de la base d'apprentissage. A partir d'un exemple de la base il est possible de créer d'autres exemples en appliquant des rotations et des retards. Ainsi on peut augmenter la taille de la base de plusieurs ordres de grandeurs sans pour autant augmenter le nombre de mesures faites sur un système OFDM. C'est cette méthode qui a été choisie, en raison de la simplicité de sa mise en oeuvre ainsi que son indépendance vis-à-vis de l'architecture du réseau de neurones utilisé.
[7] la fonction
 n'est définie que sur
n'est définie que sur 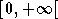 mais comme sa dérivée est nulle en
mais comme sa dérivée est nulle en  on peut la prolonger sur
on peut la prolonger sur 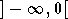 en la supposant paire, afin de simplifier l'expression du
développement en série entière
en la supposant paire, afin de simplifier l'expression du
développement en série entière