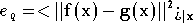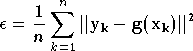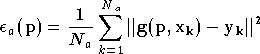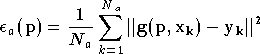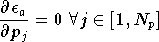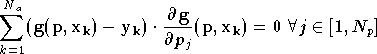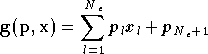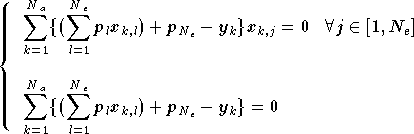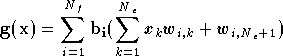Supposons que l'on veuille étudier un phénomène physique donné. L'état de ce phénomène peut être représenté par une série de grandeurs, que l'on peut regrouper dans un vecteur appelé vecteur de sortie, et noté 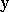. Cet état dépend de plusieurs paramètres extérieurs, que l'on peut regrouper dans un autre vecteur, appelé vecteur d'entrée, et noté . On supposera que le phénomène n'a pas de mémoire, c'est à dire que sa sortie 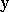à un instant donné ne dépend que de son entrée à ce même instant et non pas des entrées précédentes. Dans ce cas on peut représenter le phénomène physique comme une fonction (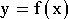) et sous forme d'un schéma-bloc :

Si l'on ne sait pas modéliser précisément le phénomène physique mais que l'on aimerait disposer d'une simulation, on peut recourir à l'approximation de fonction. Le but est de créer une nouvelle fon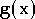ction, , que l'on connaît parfaitement et qui représentera au mieux possible la fonction 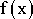. On définit une mesure de l'écart entre les deux fonctions, que l'on appelle performance^[5]. La performance la plus utilisée est l'erreur quadratique :

N'ayant pas accès à la fonction 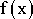, cette performance ne pourra pas être calculée. Par contre on dispose d'un jeu de mesures du phénomène physique que l'on peut représenter par une série de couples 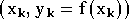. Dans ce cas il est possible de calculer une performance approchée, avec ces couples de mesures. Pour l'erreur quadratique, il s'agit de l'erreur quadratique moyenne :

L'approximation de fonction sera faite à l'aide de ce jeu de mesures, et l'on cherchera la fonction 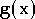qui minimise la fonction de performance .

La fonction 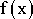doit vérifier certaines propriétés pour être approximée. Un exemple intéressant est donné dans [BOSM96] : supposons que 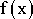soit le répertoire téléphonique, qui associe un numéro de téléphone 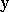au nom du propriétaire . On peut disposer du répertoire téléphonique d'une ville, qui correspond à un jeu de mesures 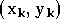. Même si l'on trouve une fonction 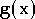qui approxime parfaitement 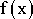, c'est à dire qui a une erreur quadratique moyenne nulle sur le jeu de mesures, l'approximation ne pourra pas donner le numéro de téléphone d'un nouvel arrivant en ville. 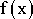Ceci est tout simplement dû au fait que la fonction n'est pas continue, et que le numéro de téléphone correspondant à un nom donné ne donne aucune information sur les numéros des noms voisins.

Plus généralement, un algorithme d'approximation a besoin que pour deux entrées voisines 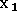et 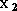les sorties correspondantes 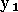et 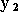soient également voisines. Les fonctions respectant cette propriété sont appelées fonctions douces ("smooth functions" en Anglais). "Fonction douce" est une notion relative, mais une définition simple que l'on peut retenir et qui suffit généralement est une fonction dérivable par morceaux et de dérivée bornée. Fort heureusement la très grande majorité des fonctions représentant des phénomènes physiques respecte cette propriété en pratique.

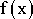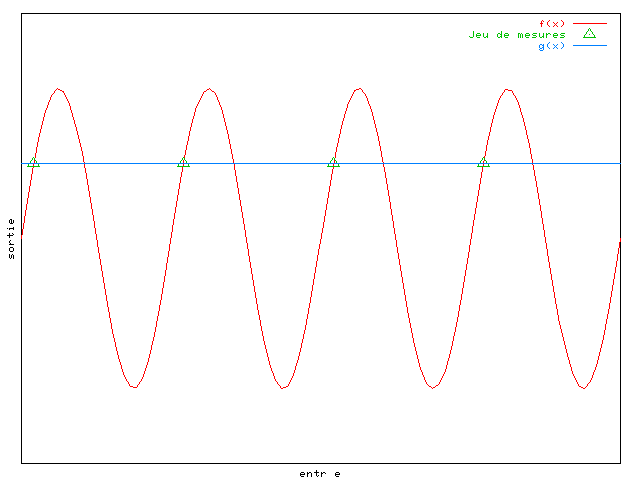
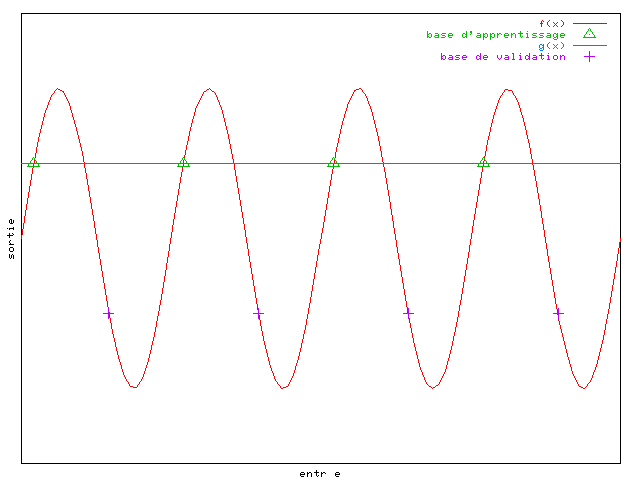
Une seconde condition porte sur le choix du jeu de données qui servira à réaliser l'approximation. Celui-ci doit être représentatif des évolutions de la fonction . Si l'on choisit le cas simple où l'on veut approximer une fonction à une dimension, sinusoïdale, et si les exemples choisis sont espacés de 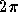, on remarque sur la figure 2.3 qu'une droite passant par les exemples peut être considérée comme une bonne approximation par l'algorithme :

En effet avec ce jeu de données, l'erreur quadratique moyenne est nulle, alors que la f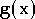onction n'est pas une bonne approximation de la sinusoïde dans l'absolu. Pour détecter ces anomalies, il est fréquent de définir deux jeux de données. Le premier, appelé base d'apprentissage, contient les données qui serviront à déterminer la fonction 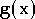. Le second, appelé base de validation, est distinct du premier, et servira simplement à vérifier que l'approximation se déroule correctement. Deux performances sont calculées, 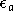avec la base d'apprentissage et 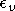avec la base de validation. On cherche à minimiser 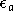et on surveille l'évolution de 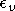. Si un écart important est constaté entre les deux performances, ceci veut dire que l'approximation n'est pas bonne, et une cause possible est un mauvais choix de la base d'apprentissage.

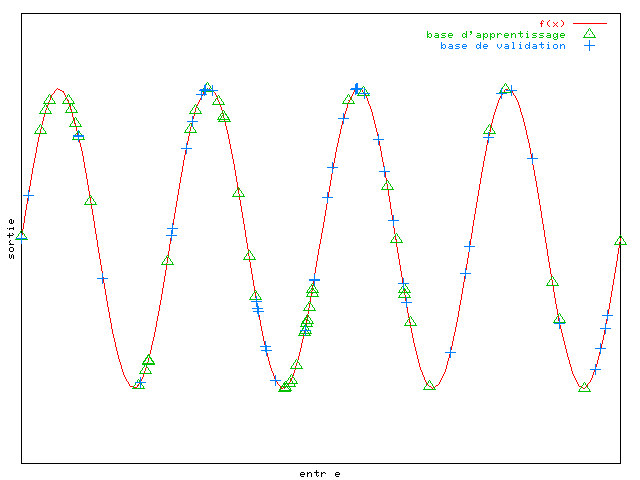
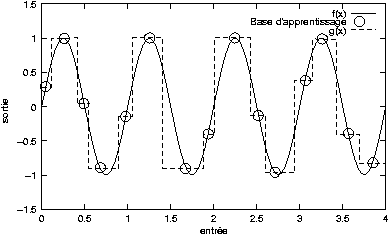
Dans l'exemple ci-dessus, avec une base de validation décalée de par rapport à la base d'apprentissage, on remarque un 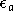nul, avec un 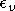élevé, ce qui est révélateur d'une base non adaptée au problème. Malheureusement il n'existe pas de critère général permettant de dire si la base d'apprentissage est bien choisie. Il est nécessaire de connaître un peu le système que l'on veut approximer, et faire quelques tests pour déterminer si le jeu de données est pertinent ou non. Dans la plupart des cas, une base constituée de vecteurs sélectionnés aléatoirement donne de bons résultats, mais le choix de la taille de la base est toujours délicat, et dépend autant de la fonction à approximer que de la méthode utilisée pour l'approximation. Par exemple pour la sinusoïde une telle base pourrait convenir :

Il existe de nombreuses méthodes d'approximation déterminant une fonction 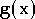qui approxime dans certaines conditions la fonct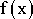ion . En pratique il n'est pas possible d'avoir un système générique, capable de créer une fonction 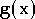de n'importe quelle forme, et donc ces méthodes se limitent à une famille de fonctions 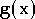possibles. Par exemple on peut envisager d'utiliser la famille des fonctions polynomiales de degré 3. On peut représenter cette famille par 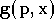où est toujours l'entrée de la fonction, et 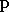est un vecteur paramètre, qui caractérise la fonction choisie dans la famille. Dans l'exemple de la famille des fonctions polynomiales de degré 3, le vecteur 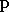sera l'ensemble des coefficients du polynôme.

Finalement, une fois la famille choisie, le problème de l'approximation devient un problème d'optimisation numérique. En effet il se réduit à trouver le vecteur de paramètres 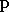qui minimise :

où 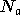est le nombre d'éléments dans la base d'apprentissage 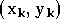. Le nombre de paramètres (la dimension du vecteur 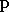) est le nombre de degrés de liberté de l'algorithme qui va déterminer la meilleure approximation. Plus ce nombre est grand, plus il sera possible de réaliser des fonctions différentes, et donc plus il sera possible d'approcher la fonction 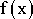. Par contre avec un nombre de degrés de liberté plus faible, la recherche de l'approximation demande moins de calcul.

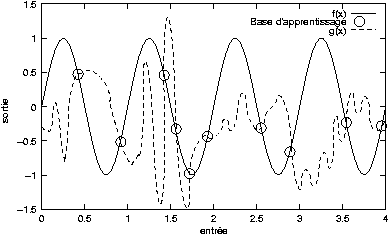
De plus si le nombre de degrés de liberté est trop élevé, un autre problème survient, celui du surapprentissage, ou apprentissage par coeur. La fonction 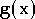obtenue est plus complexe que la fonction d'origine, et est parfaitement égale à celle-ci aux points définis par les exemples fournis. Mais 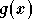ne généralise pas correctement, c'est à dire que les deux fonctions diffèrent beaucoup entre les points définis par la base d'apprentissage. Un exemple de ce phénomène de surapprentissage est illustré par la figure 2.6 :

Dans ce cas également le surapprentissage peut être détecté en définissant une seconde base, la base de validation, et en étudiant l'évolution de la performance sur cette seconde base. Pour éviter ce problème il faut limiter le nombre de degrés de liberté (tout en garantissant que les fonctions 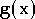pourront être assez complexes pour approximer correctement ) et augmenter la taille de la base d'apprentissage.

Avant de présenter les techniques neuronales pour l'approximation de fonction, qui sont l'objet principal de ce chapitre, nous présenterons brièvement quelques méthodes classiques d'approximation.

Le but n'est pas d'énumérer toutes les méthodes d'approximation de fonctions, mais simplement d'en citer quelques unes, utilisant une approche paramétrique. Leur point commun est de dépendre d'un vecteur de paramètres, et la méthode consiste à trouver le vecteur paramètre permettant de trouver la meilleure approximation possible.

Une première méthode est celle des moindres carrés. On choisit une famille simple de fonctions qui dépendent du vecteur paramètre 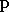, et on détermine le minimum de la fonction d'erreur quadratique moyenne :

Ce minimum est déterminé en cherchant l'extremum de cette fonction, c'est-à-dire le vecteur 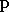pour lequel toutes les dérivées partielles s'annulent :

où 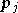est la 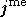composante de 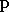, et 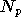est le nombre de paramètres (c'est à dire la dimension de 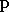). On doit donc résoudre le système d'équations suivant :

La méthode des moindres carrés est assez simple à mettre en place. Cependant elle n'est efficace qu'avec des familles de fonctions 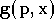simples, c'est à dire telles que la fonction de performance 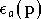ne présente qu'un seul extremum. Il est donc difficile d'appliquer cette méthode à des fonctions plus complexes, comme certains polynômes. De plus elle nécessite de connaître des informations a priori sur la forme de 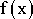pour déterminer une famille de fonctions adaptée.

D'autres méthodes qui nécessitent moins de connaissances sur la fonction réelle réalisent des approximations locales. L'espace d'entrée est découpé en zones, et sur chaque zone la fonction est approximée par une fonction simple. L'utilisation la plus simple de cette méthode est l'approximation localement constante, dans laquelle chaque zone est approximée par une constante. En dimension 1, ceci donne des fonctions en escalier :

Pour avoir des modèles plus fins il est possible de choisir des fonctions légèrement plus complexes, comme les polynômes. Dans la méthode dite des splines [BOOR78], des polynômes de degré fixe (3 en général, mais des applications existent également avec des degrés 4,5 voire 6) permettent de réaliser des approximations plus fines et de garantir la continuité de l'approximation lors du passage d'une zone à l'autre. Ces méthodes sont très efficaces, mais le choix du nombre de zones et de leurs découpages dépend de l'application et peut s'avérer délicat.

Enfin la méthode "projection pursuit" [FRIE81] approxime la fonction 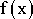par une somme de fonctions unidimensionnelles. Le vecteur d'entrée subit une série de projections linéaires, chaque projection est fournie à une fonction, et les valeurs des fonctions sont sommées. L'expression de la fonction 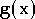est la suivante :

où 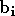sont des fonctions de base de l'approximation, 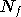est le nombre de fonctions de base à utiliser, et 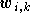sont les paramètres ajustables. 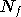doit être précisé manuellement, et dépend de la complexité de la fonction à approximer. Ensuite les paramètres 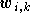sont ajustés par un algorithme d'apprentissage. On peut montrer que cette méthode est capable d'approximer n'importe quelle fonction douce, pourvu que l'on choisit un 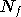assez grand. En pratique on constate de bonnes performances même avec des 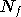faibles, en particulier dans les cas où de la redondance est présente dans l'espace d'entrée, c'est-à-dire lorsque tous les vecteurs utilisés n'occupent qu'un sous-espace de l'espace d'entrée (par exemple un plan dans un espace à 3 dimensions). Cependant les paramètres 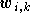sont difficiles à optimiser et les algorithmes d'apprentissage demandent beaucoup de calcul, sans garantir de trouver la solution optimale.