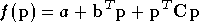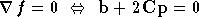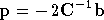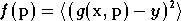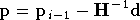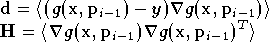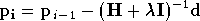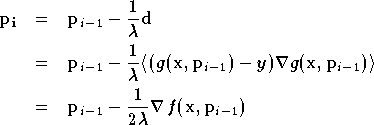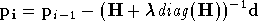Une autre manière de diminuer le nombre d'itérations d'un
algorithme d'optimisation est d'utiliser les
dérivées secondes de 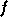 .
En effet le gradient
donne une direction vers laquelle se déplacer pour trouver le minimum,
mais ne donne pas le pas. Dans la descente de gradient classique ce pas
est un coefficient fixe, et dans la variante adaptative il peut varier à
chaque itération. Mais la dérivée seconde de
.
En effet le gradient
donne une direction vers laquelle se déplacer pour trouver le minimum,
mais ne donne pas le pas. Dans la descente de gradient classique ce pas
est un coefficient fixe, et dans la variante adaptative il peut varier à
chaque itération. Mais la dérivée seconde de
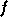 est
liée au rayon
de courbure de la fonction, et permet donc de déterminer ce pas de manière
plus fine.
est
liée au rayon
de courbure de la fonction, et permet donc de déterminer ce pas de manière
plus fine.
En effet si l'on suppose que f est une fonction quadratique :
où 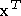 est la transposée du vecteur
est la transposée du vecteur  et
et 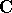 est une matrice symétrique, on peut trouver l'extremum de la fonction,
il s'agit du point auquel la dérivée de
est une matrice symétrique, on peut trouver l'extremum de la fonction,
il s'agit du point auquel la dérivée de
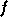 s'annule :
s'annule :
Soit :
A condition que 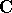 soit inversible. Pour une fonction
soit inversible. Pour une fonction 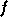 quelconque, il est possible de l'approximer localement en un point
quelconque, il est possible de l'approximer localement en un point
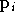 par une fonction quadratique, en utilisant ses dérivées première et
seconde, et avec l'équation (A.6)
déterminer le vecteur pour l'itération suivante d'un algorithme
d'optimisation plus évolué que la descente de gradient. Mais le calcul
des dérivées secondes peut être très long, tout d'abord parce que le
nombre de dérivées secondes est le carré de celui des dérivées premières,
et également parce que la dérivée seconde de
par une fonction quadratique, en utilisant ses dérivées première et
seconde, et avec l'équation (A.6)
déterminer le vecteur pour l'itération suivante d'un algorithme
d'optimisation plus évolué que la descente de gradient. Mais le calcul
des dérivées secondes peut être très long, tout d'abord parce que le
nombre de dérivées secondes est le carré de celui des dérivées premières,
et également parce que la dérivée seconde de
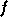 peut
être assez complexe. De nombreux algorithmes, peut-être abusivement
appelés algorithmes d'ordre 2, utilisent en fait une approximation des
dérivées secondes calculées à partir de dérivées premières. Cependant ils
gardent l'avantage de nécessiter beaucoup moins d'itérations
qu'une descente de gradient.
peut
être assez complexe. De nombreux algorithmes, peut-être abusivement
appelés algorithmes d'ordre 2, utilisent en fait une approximation des
dérivées secondes calculées à partir de dérivées premières. Cependant ils
gardent l'avantage de nécessiter beaucoup moins d'itérations
qu'une descente de gradient.
L'algorithme de
Levenberg Marquardt [MARQ63]
fait partie de ces algorithmes, et s'applique au cas particulier où
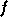 est
une
erreur quadratique moyenne. On peut donc l'exprimer sous la
forme :
est
une
erreur quadratique moyenne. On peut donc l'exprimer sous la
forme :
où 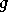 désigne une fonction de deux vecteurs
désigne une fonction de deux vecteurs  et
et 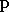 et
et 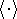 désigne la moyenne calculée sur un ensemble de couples
désigne la moyenne calculée sur un ensemble de couples
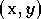 .
L'on se place dans le cas où
.
L'on se place dans le cas où 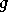 est une fonction scalaire afin de simplifier la notation, mais la même
démarche peut être faite si
est une fonction scalaire afin de simplifier la notation, mais la même
démarche peut être faite si 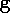 est une fonction vectorielle. Dans la suite de cette section toutes les
dérivées sont en fonction du vecteur
est une fonction vectorielle. Dans la suite de cette section toutes les
dérivées sont en fonction du vecteur 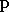 .
C'est en effet uniquement ce vecteur que l'on fait varier afin de
trouver le minimum de
.
C'est en effet uniquement ce vecteur que l'on fait varier afin de
trouver le minimum de 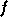 .
.
On suppose, comme pour la descente de gradient, que l'on se
trouve à une itération numéro 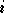 ,
et que l'on cherche à calculer un nouveau vecteur
,
et que l'on cherche à calculer un nouveau vecteur
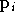 en fonction de
en fonction de 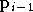 ,
tel que
,
tel que 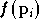 se rapproche plus d'un minimum local de
se rapproche plus d'un minimum local de
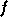 . Pour
cela on calcule une approximation quadratique
. Pour
cela on calcule une approximation quadratique
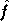 de
de 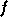 à
partir d'une approximation linéaire
à
partir d'une approximation linéaire 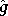 de
de 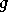 autour du point
autour du point 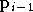 .
En déterminant le point
.
En déterminant le point 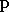 auquel le gradient de
auquel le gradient de 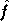 s'annule, on obtient :
s'annule, on obtient :
avec :
à condition que  soit inversible. La matrice
soit inversible. La matrice  est une approximation du Hessien de
est une approximation du Hessien de 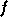 ,
calculée à partir du gradient de
,
calculée à partir du gradient de 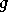 .
L'équation précédente pourrait servir dans un algorithme
d'optimisation, qui permet de calculer
.
L'équation précédente pourrait servir dans un algorithme
d'optimisation, qui permet de calculer
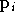 à partir de
à partir de 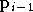 au cours de l'itération
au cours de l'itération 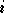 .
Mais ceci n'est efficace en pratique que si
.
Mais ceci n'est efficace en pratique que si
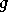 est
effectivement proche d'une droite autour du point
est
effectivement proche d'une droite autour du point
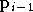 .
Dans le cas contraire cet algorithme donne de très mauvais résultats.
.
Dans le cas contraire cet algorithme donne de très mauvais résultats.
L'idée de Levenberg est donc d'utiliser cette approche
quadratique dans les zones où 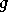 est quasi-linéaire, et une descente de gradient dans les autres cas. Le
pas d'une itération de cet algorithme est calculé de la manière
suivante :
est quasi-linéaire, et une descente de gradient dans les autres cas. Le
pas d'une itération de cet algorithme est calculé de la manière
suivante :
Lorsque 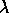 est faible, cette équation est équivalente à (A.8), et le nouveau vecteur de
paramètres est déterminé avec l'approximation quadratique de
est faible, cette équation est équivalente à (A.8), et le nouveau vecteur de
paramètres est déterminé avec l'approximation quadratique de
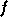 .
Lorsque
.
Lorsque 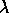 est grand, cette équation est équivalente à :
est grand, cette équation est équivalente à :
Ce qui correspond bien à une descente de gradient. Pour des valeurs
intermédiaires de 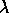 l'algorithme est un mélange entre la descente de gradient et
l'approche quadratique basée sur l'approximation linéaire de
l'algorithme est un mélange entre la descente de gradient et
l'approche quadratique basée sur l'approximation linéaire de
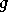 . Ce
coefficient
. Ce
coefficient 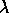 est modifié à chaque itération, comme pour la descente de gradient
adaptative. Si
est modifié à chaque itération, comme pour la descente de gradient
adaptative. Si 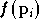 diminue au cours de l'itération, on diminue
diminue au cours de l'itération, on diminue
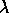 (en le divisant par 10 par exemple), et l'on se rapproche ainsi de la
méthode quadratique. Au contraire si
(en le divisant par 10 par exemple), et l'on se rapproche ainsi de la
méthode quadratique. Au contraire si 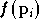 augmente, cela signifie que nous nous trouvons dans une région dans
laquelle
augmente, cela signifie que nous nous trouvons dans une région dans
laquelle 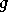 n'est pas très linéaire, et donc on augmente
n'est pas très linéaire, et donc on augmente
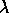 (en le multipliant par 10 par exemple) afin de se rapprocher de la
descente de gradient.
(en le multipliant par 10 par exemple) afin de se rapprocher de la
descente de gradient.
Cet algorithme a ensuite été amélioré par Marquardt, le pas de l'itération étant défini cette fois par :
La matrice identité a été remplacée par la diagonale de
 .
Le but est ici de modifier le comportement de l'algorithme dans les
cas où
.
Le but est ici de modifier le comportement de l'algorithme dans les
cas où 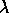 est grand, c'est à dire lorsque l'on est proche d'une descente
de gradient. Avec cette modification l'on se déplace plus vite dans
les directions vers lesquelles le gradient est plus fiable, afin
d'éviter de passer de nombreuses itérations sur un
plateau. Ceci est appelé
l'algorithme de Levenberg Marquardt.
est grand, c'est à dire lorsque l'on est proche d'une descente
de gradient. Avec cette modification l'on se déplace plus vite dans
les directions vers lesquelles le gradient est plus fiable, afin
d'éviter de passer de nombreuses itérations sur un
plateau. Ceci est appelé
l'algorithme de Levenberg Marquardt.
En pratique cet algorithme, en particulier dans le cas des réseaux
de neurones, permet de converger avec beaucoup moins
d'itérations. Mais
chaque itération demande plus de calculs, en particulier pour
l'inversion de la matrice  ,
et son utilisation se limite donc aux cas où le nombre de paramètres à
optimiser n'est pas très élevé. En effet le nombre d'opérations
nécessaires à l'inversion d'une matrice est proportionnel à
,
et son utilisation se limite donc aux cas où le nombre de paramètres à
optimiser n'est pas très élevé. En effet le nombre d'opérations
nécessaires à l'inversion d'une matrice est proportionnel à
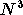 ,
,
 étant
la taille de la matrice, et ici également la taille du vecteur
étant
la taille de la matrice, et ici également la taille du vecteur
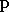 .
.